Unlocking the Spin: Exploring Rotational Motion in AP Physics 1

Have you ever wondered about the physics behind a spinning top, a rolling wheel, or the Earth's rotation? These captivating phenomena are all governed by the principles of rotational motion, a cornerstone of AP Physics 1. Understanding this area of physics opens a door to comprehending a vast array of natural processes and engineered systems.

Rotational motion, unlike linear motion, deals with the movement of objects around an axis. Instead of simply moving in a straight line, objects in rotational motion trace circular paths. This seemingly simple difference introduces a whole new set of physical quantities like torque, angular velocity, and moment of inertia, which are crucial for analyzing and predicting rotational behavior.

AP Physics 1 introduces students to the fundamental concepts of rotational motion, providing a foundation for more advanced physics courses and real-world applications. From understanding the motion of celestial bodies to designing efficient engines and understanding the stability of structures, a grasp of rotational dynamics is indispensable.

Historically, the study of rotational motion dates back to antiquity, with early astronomers observing the cyclical movements of the stars and planets. Over centuries, scientists like Galileo and Newton contributed significantly to our understanding of rotational motion, formulating the laws and equations that govern this intricate physical phenomenon. The importance of rotational motion in AP Physics 1 stems from its wide applicability across diverse fields like engineering, astronomy, and even sports.

One of the main challenges students face with rotational motion is understanding the analogous relationships between linear and rotational quantities. For instance, linear velocity corresponds to angular velocity, force corresponds to torque, and mass corresponds to moment of inertia. Mastering these parallels is key to successfully navigating the intricacies of rotational motion.

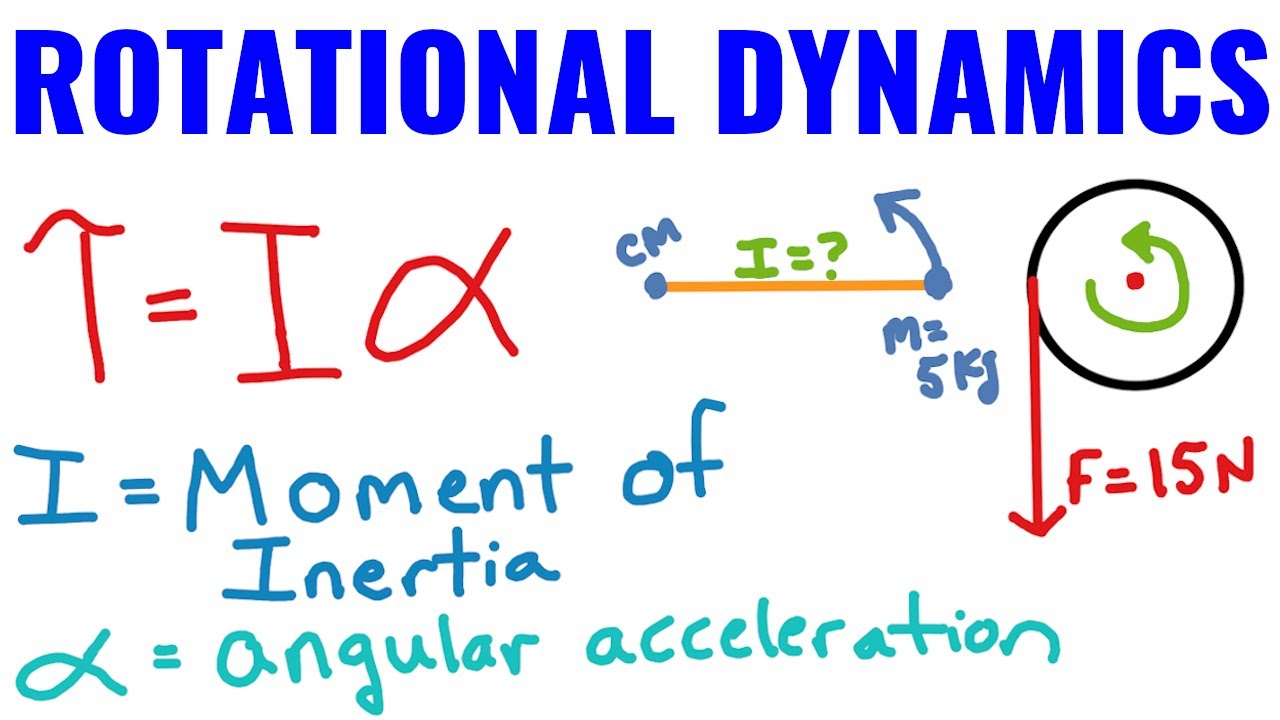
Angular velocity, often denoted by the Greek letter omega (ω), describes how fast an object rotates. It's measured in radians per second. Torque, analogous to force in linear motion, represents the rotational force applied to an object. Moment of inertia, represented by I, describes an object's resistance to changes in its rotational motion, similar to how mass represents resistance to changes in linear motion.

A simple example of rotational motion is a spinning wheel. The angular velocity describes how many radians the wheel rotates through each second. Applying a torque to the wheel will cause it to accelerate its rotation, while a larger moment of inertia would make it harder to change the wheel's spinning speed.

One benefit of studying rotational motion is the ability to analyze complex systems like gears and pulleys, which are essential components in many machines. Understanding rotational dynamics allows engineers to design more efficient and powerful systems. Another benefit is the ability to predict the trajectories of spinning objects, crucial in sports like baseball and basketball. Finally, grasping rotational motion allows us to understand the stability of structures, helping architects and engineers design buildings that can withstand external forces.

To master rotational motion in AP Physics 1, start by reviewing the key concepts of angular velocity, torque, and moment of inertia. Practice solving problems involving these quantities, gradually increasing the complexity. Focus on understanding the analogies between linear and rotational motion.

Real-world examples of rotational motion abound, from the spinning of a figure skater to the rotation of a turbine in a power plant. Other examples include the motion of a gyroscope, the wheels of a car, and the Earth's rotation about its axis. Studying these examples can deepen your understanding of the principles of rotational motion.

Advantages and Disadvantages of Focusing Heavily on Rotational Motion

While rotational motion is crucial, overemphasis can present challenges. A balanced approach is essential.

Frequently Asked Questions about Rotational Motion in AP Physics 1:

1. What is the difference between angular velocity and linear velocity? Angular velocity measures the rate of rotation, while linear velocity measures the rate of change of position in a straight line.

2. How is torque calculated? Torque is the product of the force applied and the lever arm.

3. What is the moment of inertia of a solid sphere? The moment of inertia of a solid sphere is (2/5)mr^2, where m is the mass and r is the radius.

4. How does rotational kinetic energy differ from linear kinetic energy? Rotational kinetic energy is the energy of an object due to its rotation, while linear kinetic energy is the energy of an object due to its linear motion.

5. What is angular momentum? Angular momentum is the rotational analog of linear momentum.

6. How does angular acceleration relate to torque? Torque is equal to the moment of inertia multiplied by the angular acceleration.

7. What is the right-hand rule for rotational motion? The right-hand rule is used to determine the direction of the angular velocity vector.

8. What are some common misconceptions about rotational motion? A common misconception is that heavier objects always rotate slower. This is not necessarily true, as the moment of inertia also depends on the distribution of mass.

One tip for mastering rotational motion is to visualize the motion and use diagrams to represent the problem. This can help you understand the direction of rotation and the forces involved. Another trick is to break down complex problems into smaller, more manageable parts.

In conclusion, rotational motion is a fundamental concept in AP Physics 1, with widespread applications in various fields. Understanding angular velocity, torque, moment of inertia, and the relationships between these quantities is essential for success in the course and beyond. Mastering rotational motion not only empowers students to solve complex physics problems but also provides a deeper understanding of the physical world around us. By dedicating time to studying this topic, practicing problem-solving, and exploring real-world examples, students can unlock the power of rotational dynamics and open doors to future academic and professional pursuits. Don't be afraid to spin your wheels – the rewards of mastering rotational motion are well worth the effort.

Oregons incremental salary landscape navigating the step system
Connecting through names exploring matching display names for couples
Unlocking the power of behr soft secret your guide to a serene sanctuary