Binärbäume im Array: Effiziente Speicherung und Zugriff
Stellen Sie sich vor, Sie könnten die komplexe Struktur eines Binärbaums in einem einfachen Array abbilden. Wie wäre es, wenn Sie durch simple Indexberechnungen auf jedes Element zugreifen könnten? Die Array-basierte Darstellung von Binärbäumen macht genau das möglich und bietet eine effiziente Alternative zu pointerbasierten Implementierungen.
Die Speicherung von Binärbäumen in Arrays ist eine Technik, die in verschiedenen Bereichen der Informatik Anwendung findet. Von der Datenbankverwaltung bis zur Spielentwicklung bietet diese Methode Vorteile in Bezug auf Speicherplatz und Zugriffsgeschwindigkeit. Doch wie funktioniert diese Darstellung genau und welche Herausforderungen gilt es zu beachten?
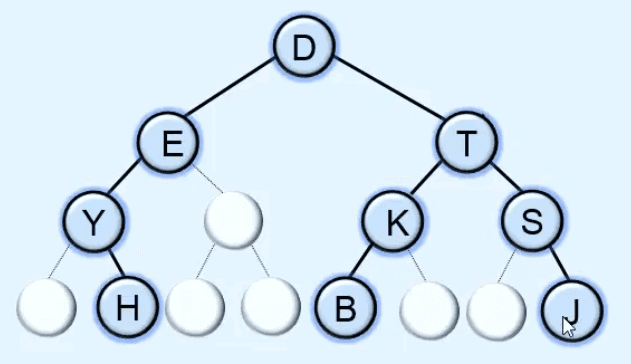
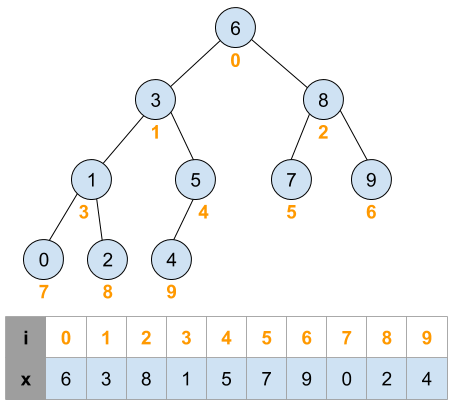
Im Kern basiert die Array-Darstellung auf einer einfachen Nummerierung der Knoten des Binärbaums. Der Wurzelknoten erhält den Index 0. Der linke Kindknoten eines Knotens an Position `i` befindet sich an Position `2i + 1`, der rechte Kindknoten an `2i + 2`. Diese Formel erlaubt eine direkte Navigation durch den Baum ohne den Einsatz von Zeigern.
Diese Methode bietet eine kompakte Speicherung, insbesondere bei vollständigen oder fast vollständigen Binärbäumen. Im Gegensatz zu Zeiger-basierten Strukturen entfällt der Overhead für die Speicherung der Zeiger selbst. Dadurch kann der Speicherbedarf reduziert und die Cache-Effizienz verbessert werden.
Allerdings birgt die Array-Darstellung auch Herausforderungen. Bei unbalancierten Bäumen kann es zu erheblicher Speicherverschwendung kommen, da Platz für nicht vorhandene Knoten reserviert werden muss. Die Umstrukturierung des Baumes, beispielsweise durch Einfügen oder Löschen von Knoten, kann ebenfalls aufwendig sein und erfordert möglicherweise das Verschieben großer Datenmengen im Array.
Die Array-Darstellung von Binärbäumen hat eine lange Geschichte in der Informatik und findet sich in vielen fundamentalen Algorithmen und Datenstrukturen wieder. Sie ist eng mit der Heap-Datenstruktur verwandt, die eine spezielle Form eines Binärbaums darstellt und oft in Arrays implementiert wird.
Ein einfacher Binärbaum mit den Werten 1 (Wurzel), 2 (links) und 3 (rechts) würde im Array wie folgt dargestellt: [1, 2, 3].
Vorteile der Array-Darstellung
Effizienter Zugriff auf Knoten über Indexberechnung.
Kompakte Speicherung bei vollständigen Bäumen.
Einfache Implementierung.
Vor- und Nachteile
| Vorteile | Nachteile |
|---|---|
| Schneller Zugriff | Speicherverschwendung bei unbalancierten Bäumen |
| Einfache Implementierung | Aufwendige Umstrukturierung |
| Kompakte Speicherung (bei vollständigen Bäumen) |
Häufig gestellte Fragen
F: Was ist eine Array-Darstellung eines Binärbaums? A: Eine Methode, einen Binärbaum in einem Array zu speichern.
F: Wie funktioniert die Indexberechnung? A: Linkes Kind: 2i + 1, rechtes Kind: 2i + 2.
F: Wann ist diese Darstellung effizient? A: Bei vollständigen oder fast vollständigen Bäumen.
F: Was sind die Nachteile? A: Speicherverschwendung bei unbalancierten Bäumen.
F: Wie fügt man einen Knoten ein? A: An der entsprechenden Indexposition im Array.
F: Wie löscht man einen Knoten? A: Durch Markieren oder Entfernen des Elements im Array.
F: Welche Alternativen gibt es? A: Zeigerbasierte Darstellungen.
F: Wo findet diese Darstellung Anwendung? A: Heap-Datenstruktur, Datenbanken, etc.
Tipps und Tricks: Bei der Implementierung sollten Sie die Größe des Arrays sorgfältig planen, um Speicherverschwendung zu minimieren. Für unbalancierte Bäume sind pointerbasierte Darstellungen oft die bessere Wahl.
Die Array-Darstellung von Binärbäumen bietet eine elegante und effiziente Methode zur Speicherung und zum Zugriff auf Baumstrukturen. Während sie bei vollständigen Bäumen ihre Stärken ausspielt, sollten die potenziellen Nachteile bei unbalancierten Bäumen berücksichtigt werden. Durch sorgfältige Planung und Abwägung der Vor- und Nachteile können Sie die optimale Darstellungsform für Ihre Anwendung wählen. Die Array-basierte Darstellung ist ein mächtiges Werkzeug im Arsenal jedes Entwicklers und ein Verständnis ihrer Funktionsweise ist unerlässlich für die Entwicklung performanter Algorithmen und Datenstrukturen. Experimentieren Sie mit dieser Methode und entdecken Sie die Möglichkeiten, die sie bietet!
Du kommst hier nicht vorbei gandalf bedeutung und einfluss des ikonischen zitats
Zellteilung mal anders einfach erklart binare spaltung
Maleah madchenname oder doch nicht die welt der namen und ihre geheimnisse
